Need: Feature selection, the process of finding and selecting the most useful features in a dataset, is a crucial step of the machine learning pipeline. Unnecessary features decrease training speed, decrease model interpretability, and, most importantly, decrease generalization performance on the test set
Approach: There are three main types of feature selection techniques: supervised and unsupervised (Dimensionality reduction based), variable importance-based methods

Filter based: Methods allow the selection or the deselection of entire features (columns, essentially) based on the passing score of some metrics. For example, if the variance (meaning that the values are too dispersed) of a column is too high, we have good reasons to avoid putting that column in the model, as it will likely diminish its accuracy. The same applies to different metrics.
- T test/Anova
- Fisher’s Score
- Correlation Coefficient
- Chi-Square Test
- Information Gain..etc

Wrapper-based: Wrapper methods group several techniques that use an R Squared value to measure whether a feature should be conserved or not. These techniques work by iteratively using features while monitoring a change in score, hence they work recursively:
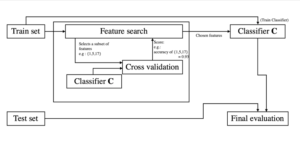
- Exhaustive Feature Selection
- Forward Regression
- Backward Regression/RFE_Recursive Feature Elimination
- Stepwise Regression
- Bi-directional elimination
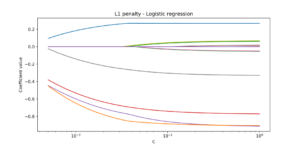
Embedded: Embedded methods are ways of performing feature selection while training the model. This is common in neural networks, where, automatically, features are selected or deselected with Normalization techniques:
- L1 Normalization
- L2 Normalization
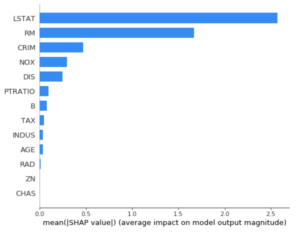
Feature importance methods: Feature importance refers to techniques that assign a score to input features based on how useful they are at predicting a target variable, Linear Regression Feature Importance,
- Regression Feature Importance
- Logistic Regression Feature Importance
- Decision Tree Feature Importance
- Random Forest Feature Importance. Etc
Dimensionality Reduction(Unsupervised Methods)
One can describe Principal Components Regression as an approach for deriving a low-dimensional set of features from a large set of variables. The idea is that the principal components capture the most variance in the data using linear combinations of the data in subsequently orthogonal directions .In this way, we can also combine the effects of correlated variables to get more information out of the available data

For code
https://github.com/drstatsvenu/feature-selection



