Need:
When conducting multiple analyses on the same dependent variable, the chance of committing a Type I error increases, thus increasing the likelihood of coming about a significant result by pure chance. To correct for this, or protect from Type I error, a Bonferroni correction is conducted.
In statistics, this is known as the family-wise error rate, which measures the probability that a Type 1 error will be made across any particular hypothesis test.
It is calculated as follows:
1 — (1-α)^n
where:
α = the significance level for a given hypothesis test
n = total number of tests
For instance, if we are using a significance level of 0.05 and we conduct three hypothesis tests, the probability of making a Type 1 error increases to 14.26%, i.e. 1-(1–0.05)³ = 0.1426.
To guard against such a Type 1 error (and also to concurrently conduct pairwise t-tests between each group), a Bonferroni correction is used whereby the significance level is adjusted to reduce the probability of committing a Type 1 error
How it will work
It is a single -step procedure and does not require a significant omnibus test to precede it
- To get the Bonferroni corrected/adjusted p value, divide the original α-value by the number of analyses on the dependent variable. Use that new alpha value to reject or accept the hypothesis
- Or multiply each reported p value by number of comparisons that are conducted

Example :
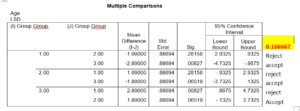
Appraoch1: Using unadjusted p vales and calculating revised alpha
Approach2: Multiplying un adjusted p values with # of tests as a corrected one
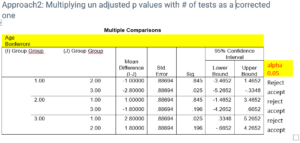
Both approaches we are getting similar conclusions.
source:
https://www.youtube.com/watch?v=rMuNniCTsOw
https://towardsdatascience.com/anova-vs-bonferroni-correction-c8573936a64e



