Need: In any classification analysis, if you want to measure the overall agreement between predicted and observed levels this measure will be very useful. Unlike Precision and Recall, and F1 score , Kappa co efficient considers perfect agreement between both predicted and observed variables in both the directions and provide the reliability measure
How it will Work
The kappa score considers how much better the agreements are over and beyond chance agreements. Thus, in addition to Agree(accuracy), the kappa formula also uses the expected proportion of chance agreements; let’s call this number Chance Agree.
Kappa Score=(Agree-Chance Agree)/(1-Chance Agree)
Note that the numerator calculates is the difference between Agree and Chance Agree. If Agree=1, we have perfect agreement, corresponding to a matrix where all the non-diagonal cells are 0. In this case, the kappa score is 1, regardless of Chance Agree. In contrast, if Agree=Chance Agree, kappa is 0, signifying that the professors’ agreement is by chance. If Agree is smaller than Chance Agree, the kappa score is negative, denoting that the degree of agreement is lower than chance agreement.
Using the Kappa Score for Classification
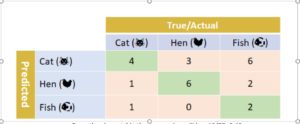
From the above table the agree value will be =12/25=0.48
And the chance agree value
- For cats = (6/25) *(13/25) =0.24*0.52=0.1248
- For Hen = (9/25) *(9/25) =0.36*0.36=0.1296
- For Fish = (3/25) * (10/25) =0.048
Change agree =0.1248+0.1296+0.048=0.3024
Now the
Kappa Score = (Agree-Chance Agree)/(1-Chance Agree)
= (0.48–0.3024)/(1–0.3024)
= 0.2546
From the above e can say that there is 25% overall agreement between predicted and observed values.
Code:
The kappa score can be calculated using Python’s scikit-learn library (R users can use the cohen.kappa() function, which is part of the psych library).
Source:



