Need: if you want to study the relationship (association) between two variables which are associated with another variable, then both RR (Relative Risk) and OR (odds ration) doesn’t work as they are able to explain the association between two variables.
(or)
If you estimate of an association between an exposure and an outcome after adjusting for or taking into account confounding. For example, experience might indicate the possibility that the relationship between some disease and a suspected risk factor differs among different ethnic groups. We would then treat ethnic membership as a confounding variable.
Solution: When identified any confounding factor, it is desirable to control for confounding variables so that an unambiguous measure of the relationship between disease status and risk factor may be calculated. A technique for accomplishing this objective is the Mantel–Haenszel Statistic
Data Layout for Cochran-Mantel-Haenszel Estimates
Before computing a Cochran-Mantel-Haenszel Estimate, it is important to have a standard layout for the two by two tables in each stratum. We will use the general format depicted here:
| Outcome Present | Outcome Absent | Total | |
| Risk Factor Present
(Exposed) |
a | b | a+b |
| Risk Factor Absent
(Unexposed) |
c | d | c+d |
| a+c | b+d | n |
Cochran-Mantel-Haenszel Equations
To explore and adjust for confounding, we can use a stratified analysis in which we set up a series of two-by-two tables, one for each stratum (category) of the confounding variable. Having done that, we can compute a weighted average of the estimates of the risk ratios or odds ratios across the strata. The weighted average provides a measure of association that is adjusted for confounding. The weighted averages for risk ratios and odds ratios are computed as follows:
Cochran-Mantel-Haenszel Estimate for a Risk Ratio
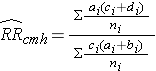
Cochran-Mantel-Haenszel Estimate for an Odds Ratio 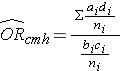
Where ai, bi, ci, and di are the numbers of participants in the cells of the two-by-two table in the ith stratum of the confounding variable, and ni represents the number of participants in the ith stratum.
Example
| Age ‹ 50 | Age ≥ 50 | |||||||
| CVD | No CVD | Total | CVD | No CVD | Total | |||
| Obese | 10 | 90 | 100 | Obese | 36 | 164 | 200 | |
| Not Obese | 35 | 465 | 500 | Not Obese | 25 | 175 | 200 | |
| Total | 45 | 555 | 600 | Total | 61 | 339 | 400 | |
Among those ‹50, the risk ratio is:
![]() Among those ≥ 50, the risk ratio is:
Among those ≥ 50, the risk ratio is:
![]()
From the stratified data we can also compute the Cochran-Mantel-Haenszel estimate for the risk ratio as follows:
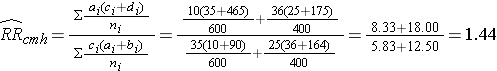
if we chose to, we could also use the same data set to compute a crude odds ratio (crude OR = 1.93) and we could also compute stratum-specific odds ratios as follows:
Among those ‹50, the odds ratio is:
![]() Among those ≥ 50, the odds ratio is:
Among those ≥ 50, the odds ratio is:
![]()
And, using the same data we could also compute the Cochran-Mantel-Haenszel estimate for the odds ratio as follows:
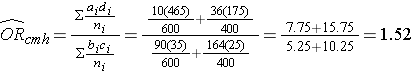
The Cochran-Mantel-Haenszel method produces a single, summary measure of association which provides a weighted average of the risk ratio or odds ratio across the different strata of the confounding factor. Notice that the adjusted relative risk and adjusted odds ratio, 1.44 and 1.52, are not equal to the unadjusted or crude relative risk and odds ratio, 1.78 and 1.93. The adjustment for age produces estimates of the relative risk and odds ratio that are much closer to the stratum-specific estimates (the adjusted estimates are weighted averages of the stratum-specific estimates).
unadjusted or crude relative risk and odds ratio
| 46 | 254 | 300 |
| 60 | 640 | 700 |
Un adjusted Weighted RR= 46/300=0.1533/60/700=0.08=1.78
Un adjusted Weighted OR= =46/254=0.181102,60/640=0.009=1.94
Source :https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704-ep713_confounding-em/BS704-EP713_Confounding-EM7.html



